ADC中的ABC：理解ADC误差对系统性能的影响 The ABCs of ADCs: Understanding How ADC Errors Affect System Performance
Abstract: Many design engineers will encounter the subtleties in ADC specifications that often lead to less-than-desired system performance. This article explains how to select an ADC based on the system requirements and describes the various sources of error when making an ADC measurement.
Using a 12-bit-resolution analog-to-digital converter (ADC) does not necessarily mean your system will have 12-bit accuracy. Sometimes, much to the surprise and consternation of engineers, a data-acquisition system will exhibit much lower performance than expected. When this is discovered after the initial prototype run, a mad scramble for a higher-performance ADC ensues, and many hours are spent reworking the design as the deadline for preproduction builds fast approaches. What happened? What changed from the initial analysis? A thorough understanding of ADC specifications will reveal subtleties that often lead to less-than-desired performance. Understanding ADC specifications will also help you in selecting the right ADC for your application.
We start by establishing our overall system-performance requirements. Each component in the system will have an associated error; the goal is to keep the total error below a certain limit. Often the ADC is the key component in the signal path, so we must be careful to select a suitable device. For the ADC, let's assume that the conversion-rate, interface, power-supply, power-dissipation, input-range, and channel-count requirements are acceptable before we begin our evaluation of the overall system performance. Accuracy of the ADC is dependent on several key specs, which include integral nonlinearity error (INL), offset and gain errors, and the accuracy of the voltage reference, temperature effects, and AC performance. It is usually wise to begin the ADC analysis by reviewing the DC performance, because ADCs use a plethora of nonstandardized test conditions for the AC performance, making it easier to compare two ICs based on DC specifications. The DC performance will in general be better than the AC performance.
System Requirements
Two popular methods for determining the overall system error are the root-sum-square (RSS) method and the worst-case method. When using the RSS method, the error terms are individually squared, then added, and then the square root is taken. The RSS error budget is given by: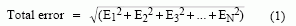
where EN represents the term for a particular circuit component or parameter. This method is most accurate when the all error terms are uncorrelated (which may or may not be the case). With worst-case error analysis, all error terms add. This method guarantees the error will never exceed a specified limit. Sinceit sets the limit of how bad the error can be, the actual error is always less than this value (often-times MUCH less).
The measured error is usually somewhere between the values given by the two methods, but is often closer to the RSS value. Note that depending on one's error budget, typical or worst-case values for the error terms can be used. The decision is based on many factors, including the standard deviation of the measurement value, the importance of that particular parameter, the size of the error in relation to other errors, etc. So there really aren't hard and fast rules that must be obeyed. For our analysis, we will use the worst-case method.
In this example, let's assume we need 0.1% or 10 bits of accuracy (1/210), so it makes sense to choose a converter with greater resolution than this. If we select a 12-bit converter, we can assume it will be adequate; but without reviewing the specifications, there is no guarantee of 12-bit performance (it may be better or worse). For example, a 12-bit ADC with 4LSBs of integral nonlinearity error can give only 10 bits of accuracy at best (assuming the offset and gain errors have been calibrated). A device with 0.5LSBs of INL can give 0.0122% error or 13 bits of accuracy (with gain and offset errors removed). To calculate best-case accuracy, divide the maximum INL error by 2N, where N is the number of bits. In our example, allowing 0.075% error (or 11 bits) for the ADC leaves 0.025% error for the remainder of the circuitry, which will include errors from the sensor, the associated front-end signal conditioning circuitry (op amps, multiplexers, etc.), and possibly digital-to-analog converters (DACs), PWM signals, or other analog-output signals in the signal path.
We assume that the overall system will have a total-error budget based on the summation of error terms for each circuit component in the signal path. Other assumptions we will make are that we are measuring a slow-changing, DC-type, bipolar input signal with a 1kHz bandwidth and that our operating temperature range is 0°C to 70°C with performance guaranteed from 0°C to 50°C.
DC Performance
Differential nonlinearity
Though not mentioned as a key parameter for an ADC, the differential nonlinearity (DNL) error is the first specification to observe. DNL reveals how far a code is from a neighboring code. The distance is measured as a change in input-voltage magnitude and then converted to LSBs (Figure 1). Note that INL is the integral of the DNL errors, which is why DNL is not included in our list of key parameters. The key for good performance for an ADC is the claim "no missing codes." This means that, as the input voltage is swept over its range, all output code combinations will appear at the converter output. A DNL error of <±1LSB guarantees no missing codes (Figure 1a). In Figures 1b, 1c, and 1d, three DNL error values are shown. With a DNL error of -0.5LSB (Figure 1b), the device is guaranteed to have no missing codes. With a value equal to -1LSB (Figure 1c), the device is not necessarily guaranteed to have no missing codes. Note that code 10 is missing. However, most ADCs that specify a maximum DNL error of +/-1 will specifically state whether the device has missing codes or not. Because the production-test limits are actually tighter than the data-sheet limits, no missing codes is usually guaranteed. With a DNL value greater than -1 (-1.5LSB in Figure 1d), the device has missing codes.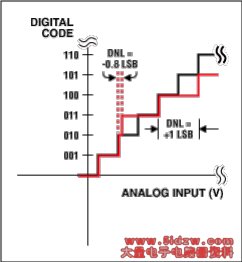
，ADC中的ABC：理解ADC误差对系统性能的影响,The A